Hyperdimensionality: The Shape of Things To Come

As an individual I have a diverse interest in anything that is related to shape and their topological design such as 3-D. The invention, the PyramiTroniX Resonator  uses the tetrahedron to accelerate the law of attration which is based on the relationship of synergetics made popular by Buckminister Fuller. I published an eBook on Synergy:Synchronized Energy and the Multiverse as a tribute honor Buckminister Fuller.
     Since, hyperbolic space is a type of non-Euclidean geometry and spherical geometry is indicative of  a constant positive curvature, hyperbolic geometry tends to address a negative curvature: where every point in hyperbolic space is a saddle point. Further, parallel lines are not uniquely paired: given a line and a point not on that line, any number of lines can be drawn through the point which are coplanar with the first and do not intersect it. This contrasts with Euclidean geometry, where parallel lines are a unique pair, and spherical geometry, where parallel lines do not exist, as all lines (which are great circles) cross each other. Another distinctive property is the amount of space covered by the n-ball in hyperbolic n-space: it increases exponentially with respect to the radius of the ball, rather than polynomially.
      Hyperbolic n-space, denoted Hⁿ, is the maximally symmetric, simply connected, n-dimensional Riemannian manifold with constant sectional curvature −1. Hyperbolic space is the principal example of a space exhibiting hyperbolic geometry. It can be thought of as the negative-curvature analogue of the n-sphere. Although hyperbolic space Hⁿ is diffeomorphic to Rⁿ its negative-curvature metric gives it very different geometric properties. Hyperbolic 2-space, H², is also called the hyperbolic plane.
     A hyperbolic 3-manifold is a 3-manifold is the quotient of three-dimensional hyperbolic space by a subgroup of hyperbolic isometries acting freely and properly discontinuously. In mathematics, a Kleinian model is a model of a three-dimensional hyperbolic manifold N by the quotient space as a non-orientable surface -- informally, a surface (a two-dimensional manifold in which notions of left and right cannot be consistently defined.
     Other related non-orientable objects include the Möbius strip and the real projective plane. Whereas a Möbius strip is a surface with boundary, a Klein bottle has no boundary. (For comparison, a sphere is is an orientable surface with no boundary.)
     
Construction

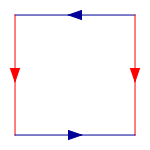
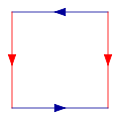
To construct the Klein bottle you begin with a a square, and then glue together corresponding coloured edges, in the following diagram, so that the arrows match. More formally, the Klein bottle is the quotient space described as the square [0,1] × [0,1] with sides identified by the relations (0, y) ~ (1, y) for 0 ≤ y ≤ 1 and (x, 0) ~ (1 − x, 1) for 0 ≤ x ≤ 1:

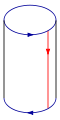
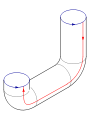
This square is a fundamental polygon of the Klein bottle. Note that this is an "abstract" gluing in the sense that trying to realize this in three dimensions results in a self-intersecting Klein bottle. The Klein bottle, proper, does not self-intersect. Nonetheless, there is a way to visualize the Klein bottle as being contained in four dimensions. Glue the red arrows of the square together (left and right sides), resulting in a cylinder. To glue the ends together so that the arrows on the circles match, pass one end through the side of the cylinder. Note that this creates a circle of self-intersection. This is an immersion of the Klein bottle in three dimensions.

• 
• 
• 
• 
• 
• 

By adding a fourth dimension to the three dimensional space, the self-intersection can be eliminated. Gently push a piece of the tube containing the intersection along the fourth dimension, out of the original three dimensional space. A useful analogy is to consider a self-intersecting curve on the plane; self-intersections can be eliminated by lifting one strand off the plane.

This immersion is useful for visualizing many properties of the Klein bottle. For example, the Klein bottle has no boundary, where the surface stops abruptly, and it is non-orientable,  as reflected in the one-sidedness of the immersion.

Klein bottle in the Science Museum in London

A hand-blown Klein Bottle

Dissecting the Klein bottle results in Möbius strips.

Properties
The Klein bottle can be seen as a fiber bundle over S¹ as follows: one takes the square (modulo the edge identifying equivalence relation) from above to be E, the total space, while the base space B is given by the unit interval in y, modulo 1~0. The projection π is then given by π([x, y]) = [y].
      Unlike the Möbius strip, the Klein bottle is a closed manifold, meaning it is a compact manifold without boundary. While the Möbius strip can be embedded in three-dimensional Euclidean Space R³, the Klein bottle cannot. It can be embedded in R⁴, however. The Klein bottle can be constructed (in a mathematical sense, because it cannot be done without allowing the surface to intersect itself) by joining the edges of two Möbius strips together.
     When embedded in Euclidean space the Klein bottle is one-sided. However there are other topological 3-spaces, and in some of the non-orientable examples a Klein bottle can be embedded such that it is two-sided, though due to the nature of the space it remains non-orientable.Its thick-thin decomposition has a thin part consisting of tubular neighborhoods of closed geodesics and/or ends which are the product of a Euclidean surface and the closed half-ray. The manifold is of finite volume if and only if its thick part is compact. In this case, the ends are of the form torus cross the closed half-ray and are called cusps
_____________________

The Mobius

A model can easily be created by taking a paper strip and giving it a half-twist, and then joining the ends of the strip together to form a loop. In Euclidean space there are two types of Möbius strips depending on the direction of the half-twist: counter or counter-clockwise.


Properties

The Möbius strip has several curious properties. A line drawn starting from the seam down the middle will meet back at the seam but at the "other side". If continued the line will meet the starting point and will be double the length of the original strip. This single continuous curve demonstrates that the Möbius strip has only one boundary.
Cutting a Möbius strip along the center line with a pair of scissors yields one long strip with two full twists in it, rather than two separate strips; the result is not a Möbius strip. This happens because the original strip only has one edge that is twice as long as the original strip. Cutting creates a second independent edge, half of which was on each side of the scissors. Cutting this new, longer, strip down the middle creates two strips wound around each other, each with two full twists.
     A strip with an odd-number of half-twists, such as the Möbius strip, will have only one surface and one boundary. A strip twisted an even number of times will have two surfaces and two boundaries.If a strip with an odd number of half-twists is cut in half along its length, it will result in a longer strip, with the same number of loops as there are half-twists in the original. Alternatively, if a strip with an even number of half-twists is cut in half along its length, it will result in two linked strips, each with the same number of twists as the original.      Whereas, the Weeks manifold, discovered in 1985 by Weeks, is the hyperbolic 3-manifold with the minimum possible volume. Weeks has written various computer programs to assist in mathematical research and mathematical visualization. His SnapPea program is used to study hyperbolic 3-manifolds, while he has also developed interactive software to introduce these ideas to middle-school, high-school, and college students.
     Weeks is particularly interested in using topology to understand the spatial universe. His book The Shape of Space: How to Visualize Surfaces and Three-dimensional Manifolds (Marcel Dekker, 1985, ISBN 0-8247-7437-X) explores the geometry and topology of low-dimensional manifolds. The second edition (2002, ISBN 0-8247-0709-5) explains some of his work in applying the material to cosmology.

http://geometrygames.org/CurvedSpaces/index.html

http://geometrygames.org/KaleidoTile/index.html